⚙️ Création de fonctions
- Fonction simple
- Paramètres
- Retour
- Portée
- Pile d'appels
- Commentaires
- Exercices
- *Récursivité*
Une fonction est un bloc de code réutilisable (un ensemble d'instructions) ayant une tâche ou un but spécifique.
Elle est définie à l'aide du mot-clé def, suivi du nom de la fonction, de parenthèses et d'un :.
Le code à l'intérieur de la fonction est indenté avec une tabulation (touche TAB).
En Python, cette indentation est essentielle pour délimiter le bloc de code de la fonction.
def saluer():
print("Bonjour!")
print("Bienvenue dans le cours SN1.")
Dans cet exemple, nous avons défini une fonction nommée saluer qui affiche "Bonjour!" lorsqu'elle est appelée.
Une fonction n'est définie (avec le mot-clé def) qu'une seule fois.
Une fois définie, la fonction peut être appelée à tout moment dans le code, en utilisant son nom suivi de parenthèses :
saluer() # 1er appel de la fonction
saluer() # 2e appel de la fonction
Appeler une fonction se fait en écrivant son nom suivi de parenthèses.
Lorsqu'une fonction est appelée, le code à l'intérieur de la fonction est exécuté.
On peut appeler une fonction autant de fois que souhaité.
La définition d'une fonction doit toujours être placée avant les appels à celle-ci.
Tenter d'appeler une fonction avant sa définition génère une erreur similaire à ceci :
NameError: name 'nom_de_la_fonction' is not defined
Les fonctions peuvent accepter des paramètres, qui sont des valeurs d'entrée que la fonction peut utiliser pour
effectuer son travail.
Lorsqu'une fonction est appelée, les valeurs transmises (les arguments) sont associées aux paramètres définis dans la fonction.
def saluer(nom):
print(f"Bonjour, {nom}!")
saluer("Alice") # Affiche "Bonjour, Alice!"
saluer("Verso") # Affiche "Bonjour, Verso!"
Dans cet exemple, la fonction saluer prend un paramètre nom et affiche un message de salutation en utilisant ce paramètre.
Si une fonction accepte plusieurs paramètres, les noms des paramètres sont séparés par une virgule.
Au niveau de l'appel, les valeurs transmises doivent aussi être séparées par une virgule en respectant l'ordre attendu.
def affiche_difference(a, b):
print(f"La différence entre {a} et {b} est {a - b}")
affiche_difference(8, 5) # Affiche "La différence entre 8 et 5 est 3"
affiche_difference(5, 1) # Affiche "La différence entre 5 et 1 est 4"
Il est possible de définir une valeur par défaut pour un paramètre.
Si aucune valeur n'est fournie pour un paramètre lors de l'appel de la fonction, la valeur par défaut sera utilisée.
def saluer(nom="inconnu"):
print(f"Bonjour, {nom}!")
saluer() # Affiche "Bonjour, inconnu!"
saluer("Alice") # Affiche "Bonjour, Alice!"
Dans cet exemple, si saluer est appelée sans valeur transmise, nom prendra la valeur par défaut "inconnu".
Une fonction peut posséder à la fois des paramètres avec des valeurs par défaut et des paramètres sans valeurs par défaut.
def saluer(nom, age, ville="Longueuil", langue="français"):
print(f"Bonjour {nom}, {age} ans, de {ville}, parlant {langue}.")
#Exemples d'appels
saluer("Renoir", 72) #Affiche "Bonjour Renoir, 72 ans, de Longueuil, parlant français".
saluer("Maelle", 16, "Laval", "anglais") #Affiche "Bonjour Maelle, 16 ans, de Laval, parlant anglais."
saluer("Sciel", 33, langue="anglais") #Affiche "Bonjour Sciel, 33 ans, de Longueuil, parlant anglais."
saluer("Gustave", 33, ville="Montréal") #Affiche "Bonjour Gustave, 33 ans, de Montréal, parlant français."
Lorsqu’on définit une fonction, il est courant de placer d’abord les paramètres obligatoires (ceux qui n’ont pas de valeur par défaut), suivis des paramètres facultatifs (ceux qui ont une valeur par défaut).
Cette organisation permet à l’utilisateur de la fonction de fournir les valeurs pour les paramètres essentiels en priorité, tout en ayant la liberté de spécifier uniquement les options supplémentaires s’il le souhaite.
La ligne #7 de l'exemple est particulièrement intéressante à analyser :
- on fournit un nom et un âge
- on ne fournit aucune valeur pour la ville, la valeur par défaut "Longueuil" sera prise.
- malgré l'absence de valeur pour la ville, on peut fournir une valeur pour la langue, ici "anglais".
Une fonction peut retourner une valeur à l'aide du mot-clé return.
Lorsqu'une fonction est appelée, elle exécute son code et renvoie la valeur spécifiée par return là où elle est appelée.
L'exécution de la fonction s'arrête dès que l'instruction return est rencontrée.
Pour cette raison, on ne place pas d'autres instructions à la suite d'un return, car elles ne seront jamais exécutées.
L'instruction return est généralement placée à la toute fin d'une fonction.
def fonction_lineaire(a, x, b):
y = a * x
y = y + b
return y
resultat = fonction_lineaire(5, 2, 5)
print(resultat) # Affiche 15
print(fonction_lineaire(3, 2, 5)) # Affiche 11
Dans cet exemple, la fonction fonction_lineaire prend les paramètres a, x et b puis calcule le y correspondant et le retourne.
La valeur retournée doit ensuite être stockée dans une variable si on souhaite la réutiliser plus tard (ici dans la variable resultat à l'aide de l'opérateur d'assignation =).
NoneUne fonction ne retourne pas toujours une valeur.
Par exemple, la fonction ci-dessous affiche simplement une salutation à la console sur 2 lignes :
def salutation(nom, age):
print("Bonjour")
print(f"Je m'appelle {nom}, j'ai {age} ans")
salutation("Gustave", 32) # La fonction ne renvoie aucune valeur
Lorsqu'une fonction retourne aucune valeur, donc absence d'une instruction return,
une valeur est tout de même retournée. Python retourne automatiquement la valeur None.
Par exemple, le code ci-dessous affiche None :
resultat = salutation("Gustave", 32) # La fonction salutation est une fonction sans return
print(resultat) # None
print(salutation("Sciel", 32)) # None
Pour cette raison, n'affichez jamais le résultat d'une fonction qui ne retourne rien!
Cela affichera toujours None, ce qui n'a aucun sens.
# bonne utilisation :
salutation("Gustave", 32) # Affiche la salutation
# mauvaise utilisation :
print(salutation("Gustave", 32)) # Affiche la salutation puis "None"
Une fonction peut aussi retourner plusieurs valeurs en les séparant par des virgules.
Lorsqu'une fonction retourne plusieurs valeurs, elles sont renvoyées sous forme de tuple (une structure de données que nous verrons plus tard).
def diviser(a, b):
quotient = a / b
reste = a % b
return quotient, reste
q, r = diviser(10, 3)
print(f"Quotient: {q}, Reste: {r}") # Affiche "Quotient: 3.3333333333333335, Reste: 1"
Dans cet exemple, la fonction diviser retourne à la fois le quotient et le reste de la division.
Ces valeurs sont ensuite assignées à deux variables distinctes, séparées par une virgule lors de l'appel de la fonction.
La portée d'une variable détermine où cette variable peut être accédée dans le code.
En Python, il existe deux types principaux de portée : locale et globale.
PORTÉE GLOBALE
Une variable définie en dehors d’une fonction est globale.
Elle peut être utilisée dans tout le programme, y compris à l’intérieur des fonctions,
sauf si une variable du même nom est définie localement (cette situation est montrée plus bas).
x = 10 # Variable globale
def ma_fonction():
print(f"Valeur de x dans la fonction : {x}") # x est accessible ici
ma_fonction()
print(f"Valeur de x en dehors de la fonction : {x}")
PORTÉE LOCALE
Une variable définie à l’intérieur d’une fonction est locale. Elle n’existe que dans cette fonction.
Les paramètres d'une fonction ont une portée locale également (ce sont comme des variables locales).
def ma_fonction(z): # z a une portée locale
y = 5 # Variable locale
print(f"Valeur de y dans la fonction : {y}")
print(f"Valeur de z dans la fonction : {z}")
ma_fonction(5)
ma_fonction(4)
# print(y) # Erreur : y n'existe pas en dehors de la fonction
# print(z) # Erreur : z n'existe pas en dehors de la fonction
Deux variables ne peuvent pas avoir le même nom dans le même espace de portée, sinon c'est la même variable!
Cependant, si 2 variables ont le même nom mais dans des espaces de portée différents (une globale et une locale), la version locale prend le dessus dans sa portée. Elle cache la variable globale, mais ne la modifie pas.
x = 10 # Variable globale
def ma_fonction():
x = 5 # Nouvelle variable locale, différente de la globale
print(f"Valeur locale de x : {x}") # Affiche 5
ma_fonction()
print(f"Valeur globale de x : {x}") # Affiche 10
👉 Dans cet exemple, la variable x à l’intérieur de la fonction est indépendante de celle à l’extérieur.
Elles ont le même nom, mais ce sont 2 variables différentes. Lorsque vous faites la trace, vous devez prévoir 2 colonnes!
Les fonctions peuvent appeler d'autres fonctions.
Cela est utile pour décomposer des tâches complexes en sous-tâches plus simples.
def ajouter(x, y):
return x + y
def multiplier(x, y):
return x * y
def calculer_expression(a, b, c):
somme = ajouter(a, b)
resultat = multiplier(somme, c)
return resultat
valeur = calculer_expression(2, 3, 4)
print(valeur) # Affiche 20
Dans cet exemple, la fonction calculer_expression appelle les fonctions ajouter et multiplier pour
effectuer une série de calculs.
Lorsque l’on démarre un programme Python, une pile d'appels est automatiquement créée.
Cette structure de données, généralement invisible sauf en cas d’erreur ou via des outils de débogage,
permet à Python de suivre l’ordre d’exécution des fonctions et de conserver l’état des variables locales.
🔁 Fonctionnement de la pile
- Lorsqu’une instruction appelle une fonction, celle-ci est empilée au sommet de la pile d'appels.
- Python exécute une seule fonction à la fois, toujours celle qui se trouve en haut de la pile.
- Une fois l’exécution terminée, la fonction est retirée de la pile.
- La fonction suivante au sommet devient alors la nouvelle fonction active, que Python exécute immédiatement.
📚 Principe LIFO
La pile d'appels suit le principe LIFO (Last In, First Out) :
- La dernière fonction ajoutée est la première à être exécutée, et la première à être retirée.
- Ce mécanisme permet à Python de gérer les appels imbriqués de fonctions, et de revenir à l’état précédent une fois qu’une fonction a terminé son exécution.
def fonction_a():
print("Fonction A")
fonction_b()
def fonction_b():
print("Fonction B")
fonction_a()
Dans cet exemple, lorsque fonction_a est appelée, elle appelle fonction_b, qui est ajoutée à la pile d'appels.
Une fois que fonction_b a terminé son exécution, le contrôle revient à fonction_a.
Le débogueur permet d'inspecter tous les détails de la pile d'appels.
Copiez le code ci-dessous dans un script, mettez un point d'arrêt sur la ligne 12 (valeur = ...) et exécutez le script en mode débogage.
def ajouter(x, y):
return x + y
def multiplier(x, y):
return x * y
def calculer_expression(a, b, c):
somme = ajouter(a, b)
resultat = multiplier(somme, c)
return resultat
valeur = calculer_expression(2, 3, 4)
print(valeur) # Affiche 20
Pour entrer dans les fonctions appelées en mode débogage, il faut utiliser le bouton Step Into .
Lorsque vous entrez dans la fonction calculer_expression, vous voyez :
- cette fonction s'ajouter au sommet de la pile d'appels (à gauche),
- les paramètres
a,betcapparaître dans la liste des variables (à droite) :
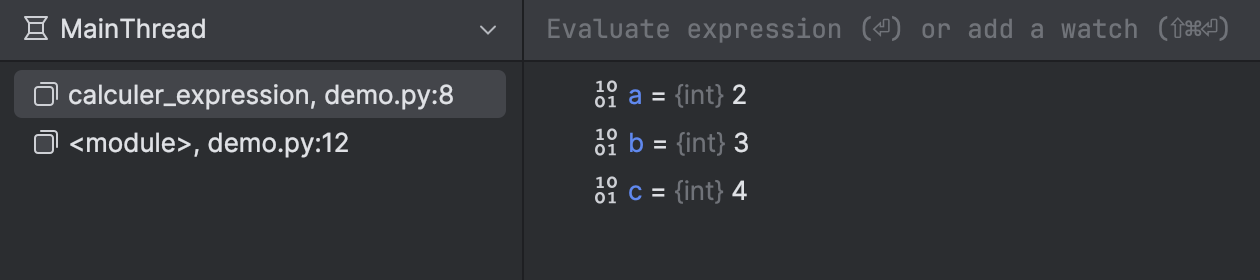
Si vous appuyez de nouveau sur , vous entrez dans la fonction
ajouter.
Vous pouvez voir que la fonction ajouter est maintenant au sommet de la pile d'appels, et les paramètres x et y sont affichés dans la liste des variables :
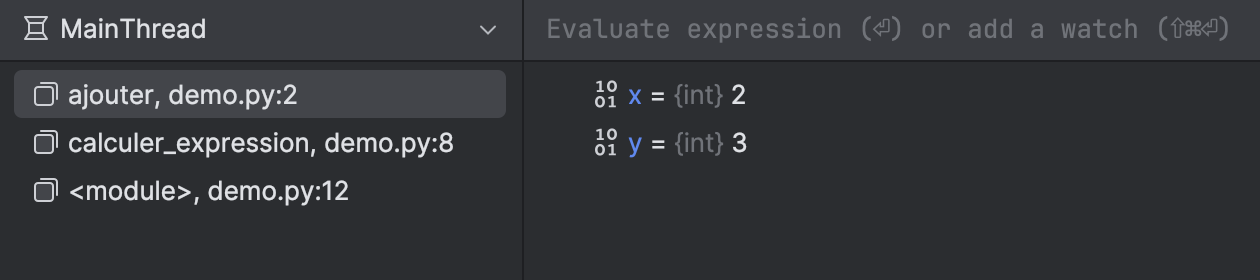
Remarquez que les paramètres a, b et c de calculer_expression ne sont plus visibles,
car vous êtes maintenant dans la fonction ajouter et a, b et c sont hors de portée.
Vous pouvez cliquer sur le nom de la fonction calculer_expression dans la pile d'appels pour revenir à cette fonction et voir ses paramètres à nouveau :
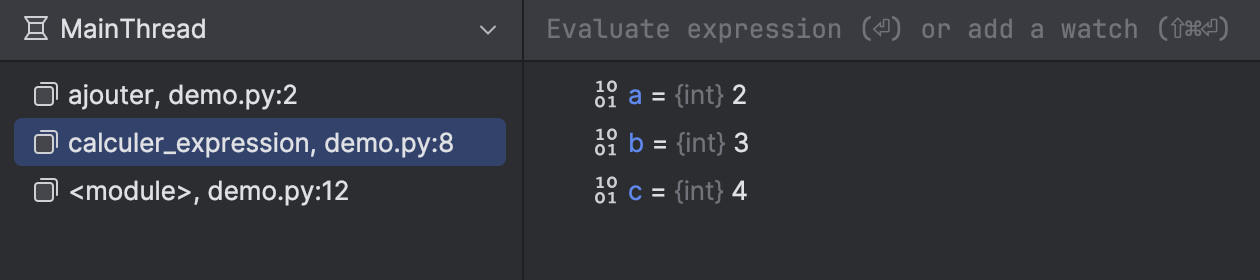
Lorsque vous faites la trace d'exécution d'un code qui contient des appels de fonctions,
il est nécessaire de noter la pile d'appels et les variables locales à chaque étape
comme dans l'exemple de trace disponible ici.
Le débogueur est alors le meilleur outil pour valider votre trace... sauf pour le volet papier de l'examen!
Il est possible d'ajouter des commentaires dans le code pour expliquer ce que fait une fonction ou pour donner des indications sur son utilisation.
Les commentaires sont ignorés par l'interpréteur Python et n'affectent pas l'exécution du code.
Ils sont utiles pour rendre le code plus lisible et compréhensible pour les autres développeurs (et pour vous-même dans le futur!).
En Python, les commentaires sont créés en utilisant le symbole # pour commenter une ligne entière ou une partie de ligne.
Pour documenter une fonction, il est possible d'utiliser les triples guillemets """ (ou ''').
Ce type de documentation se nomme un docstring et est toujours placé au début de la définition d'une fonction.
Créer une fonction sans mettre une documentation est une mauvaise pratique!
Par exemple :
# Ceci est un commentaire sur une seule ligne
def energie_cinetique(masse, vitesse): # Ceci est un commentaire en fin de ligne
"""
Calcule l'énergie cinétique d'un objet en mouvement.
Formule :
E_c = 0.5 * m * v^2
Paramètres :
masse (float) : Masse de l'objet en kilogrammes (kg)
vitesse (float) : Vitesse de l'objet en mètres par seconde (m/s)
Retourne :
float : Énergie cinétique en Joules (J)
Exemple d'utilisation :
>>> energie_cinetique(10, 5)
125.0
"""
nb_joute = 0.5 * masse * pow(vitesse,2)
return nb_joute
# Exemple avec différentes valeurs
objet1 = energie_cinetique(2, 3) # Masse de 2 kg, vitesse de 3 m/s
objet2 = energie_cinetique(5, 7) # Masse de 5 kg, vitesse de 7 m/s
# Affichage des résultats
print("Énergie cinétique de l'objet 1 :", objet1, "Joules")
print("Énergie cinétique de l'objet 2 :", objet2, "Joules")
Les lignes 3 à 19 montrent un exemple de commentaire de bloc utilisant des triples guillemets pour expliquer en détail la fonction energie_cinetique.
Lorsqu'une fonction possède une documentation sous forme de docstring, l'IDE vous permet de visualiser cette documentation rapidement.
Par exemple, si vous placez votre souris sur l'un des deux appels de fonction energie_cinetique, la documentation sera affichée.
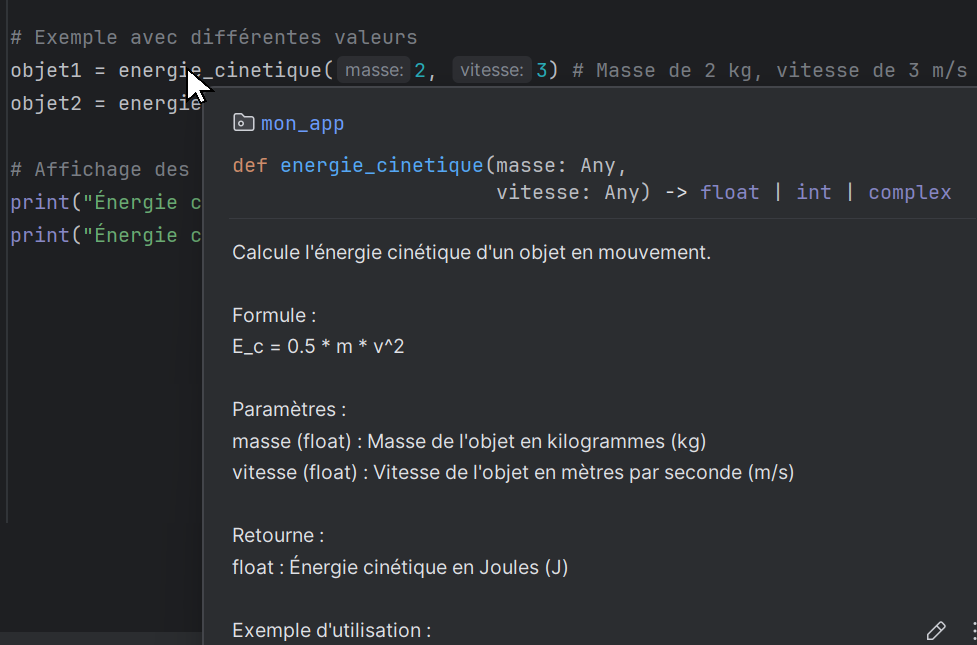
Les docstrings servent qu'à la documentation et elles sont ignorées par Python lors de l'exécution du code.
Il en est de même pour les lignes 1, 23 et 27 qui sont des commentaires sur une seule ligne, ainsi que tout ce qui se trouve à droite du # à la ligne 2.
🧠 Auto-validation des connaissances
Ce formulaire sert à vérifier votre compréhension des éléments les plus importants de la rencontre R03. Ne faites ce questionnaire que lorsque vous vous sentez en très bonne maîtrise de la matière. En classe, dès votre arrivée, vous aurez un questionnaire très similaire, évalué sommativement, à compléter sans accès à aucune documentation.
Ne pas remplir le formulaire diminue fortement vos chances de réussir l’évaluation sommative en début de rencontre.
Assurez-vous de bien comprendre toutes les notions derrière chaque question.
✏️ Exercices de compréhension
Pour le premier exercice de cette section, vous pouvez écrire vos réponses sur papier ou vous pouvez créer un fichier markdown.
Pour les autres exercices, vous pouvez imprimer ce tableau de trace d'exécution pour réaliser les traces.
Il n’y a aucune trace à rédiger pour ce numéro.
Soit le code suivant :
def calcul_complexe(a, b, c):
x = a ** b
y = c * (b - a)
return a ** b + c * (b - a)
x = 5
calcul_complexe(3, 5, 7)
print(x)
Combien vaut x dans calcul_complexe? (ligne 2)
Combien vaut x dans le script principal? (ligne 6)
S’agit‑il de la même variable 𝑥 ou de deux variables distinctes? Expliquez.
Sans exécuter le code, qu'affichera le programme ci-dessous?
En suivant cette recette, faites la trace de l'exécution de ce code :
En situation d'examen, ce type de question serait à faire sans l'ordinateur.
def fonction_lineaire(a, x, b) :
print("appel de la fonction")
resultat = a * x + b
return resultat
x = 5
y = 10
z = 2
r1 = fonction_lineaire(x, z, y) # Attention à l'ordre des paramètres
x = x - 3
r2 = fonction_lineaire(x, y, z)
print(r1, r2)
Validez votre trace en exécutant le code dans un script en mode débogage.
En suivant cette recette, faites la trace de l'exécution de ce code :
def ajoute_cinq(x):
print("appel de ajoute_cinq")
return x + 5
def carre(x):
print("appel de carre")
return x * x
def calcul_final(a, b):
print("appel de calcul_final")
return carre(a) + ajoute_cinq(b)
x = 2
y = 3
resultat = calcul_final(x, y)
print(resultat)
Validez votre trace en l'exécutant en mode débogage.
🔨 Exercices de création
Pour chacun des exercices de cette section, vous devez créer des fichiers .py avec un nom significatif.
À partir de maintenant, n'utilisez plus la fonction input, sauf lorsque c'est clairement indiqué dans l'énoncé.
Si un numéro nécessite l'utilisation de la fonction input, ça sera clairement indiqué dans les instructions du numéro.
Écrivez une fonction dire_bonjour() qui affiche simplement le message "Bonjour!" dans la console.
Ensuite, modifiez la fonction pour qu’elle prenne un paramètre prenom et affiche :
Bonjour, Alice!
lorsqu’on appelle dire_bonjour("Alice").
Écrivez une fonction celsius_vers_fahrenheit(celsius) qui reçoit une température en °C et retourne sa valeur
en °F grâce à la formule
Tester votre fonction à l'aide des instructions ci-dessous :
print(celsius_vers_fahrenheit(0)) # 32.0
print(celsius_vers_fahrenheit(100)) # 212.0
Écrivez une fonction aire_rectangle(longueur, largeur) qui calcule et retourne l’aire d’un rectangle.
Puis, appelez la fonction pour afficher l’aire d’un rectangle de 5 m 3 m. Par exemple :
print(f"L'aire d'un rectangle de 5 x 3 est : {aire_rectangle(5,3)}") # L'aire d'un rectangle de 5 x 3 est : 15
-
Écrivez une fonction
aire_rectangle(longueur, largeur)qui calcule et retourne l’aire d’un rectangle. -
Écrivez une deuxième fonction
volume_prisme(longueur, largeur, hauteur)qui calcule et retourne le volume d’un prisme rectangulaire.
👉 Cette deuxième fonction doit réutiliser (appeler) votre fonction aire_rectangle pour calculer la base du prisme avant de la
multiplier par la hauteur.
- Testez vos fonctions en affichant :
- l’aire d’un rectangle de
- le volume d’un prisme de
Objectif : pratiquer la décomposition d’un problème en plusieurs fonctions réutilisables.
Pour cet exercice, vous devez créer un module (un fichier .py) et un script (un autre fichier .py).
Référez-vous à la recette sur les modules pour savoir comment faire.
Le module doit contenir une fonction, et le script doit importer ce module pour utiliser la fonction.
- Dans le module, nommé
sciences_nature, écrivez une fonction permettant de calculer l'énergie cinétique en utilisant la formule :
où est la masse et la vitesse.
- Dans le script (un autre fichier
.py) :- importez le module,
- appelez votre fonction avec différentes valeurs,
- affichez les résultats.
Dans le même module créé à l'exercice précédent, ajoutez une fonction permettant de calculer la force gravitationnelle en utilisant la loi de la gravitation universelle de Newton dont la formule est :
où :
- (constante gravitationnelle),
- et sont les masses en kg,
- est la distance en mètres.
Dans un script Python (ça peut être le même qu'à l'exercice précédent) :
- importez le module,
- appelez votre fonction avec différentes valeurs,
- affichez les résultats.
Le code ci-dessous affiche un rapport concernant des expérimentations réalisées par une entreprise pharmaceutique de confiance.
Beaucoup d'instructions servant a afficher des données sont très similaires et sont utilisées dans le même ordre.
En programmation, c'est un signe qu'on doit créer une fonction!
Améliorez ce code! Définissez une fonction et appelez-la.
print("Rapport - Résultats des expériences Umbrella Corporation")
print("Échantillon : Virus-T")
print("Température : 37.0°C")
print("pH : 6.2")
print("Mutation Cellulaire : Stable")
print("Contagiosité : Élevée")
print("---------------")
print("Échantillon : Virus-G")
print("Température : 39.5°C")
print("pH : 5.8")
print("Mutation Cellulaire : Instable")
print("Capacité Régénérative : Extrême")
print("---------------")
print("Échantillon : Uroboros")
print("Température : 40.0°C")
print("pH : 7.0")
print("Mutation Cellulaire : Agressive")
print("Compatibilité Hôte : Faible")
print("---------------")
print("Fin du rapport. Données classifiées - Niveau d'accès : Alpha")
Lorsqu'on exécute la version originale du code, ou votre version améliorée, on devrait observer le même résultat dans la console.
Le code ci-dessous permet de calculer la densité en kg/m3 de 3 échantillons pour lesquels nous possédons une masse en g et un volume en cm3.
Le calcul de la densité nécessite plusieurs instructions. Simplifiez ce code en créant une fonction pour calculer la densité en kg/m3 et appelez-la.
⚠️ Il est INTERDIT de modifier les instructions 1 à 7 et 20 à 23, inclusivement.
#Variables contenants les données de 3 échantillons
echantillon1_masse_en_g = 135
echantillon1_volume_cm3 = 84
echantillon2_masse_en_g = 270
echantillon2_volume_cm3 = 151
echantillon3_masse_en_g = 92
echantillon3_volume_cm3 = 113
#Calcul des densitées pour les 3 échantilllons
echantillon1_masse_en_kg = echantillon1_masse_en_g / 1000
echantillon1_volume_m3 = echantillon1_volume_cm3 / 1_000_000
echantillon1_densite = echantillon1_masse_en_kg / echantillon1_volume_m3
echantillon2_masse_en_kg = echantillon2_masse_en_g / 1000
echantillon2_volume_m3 = echantillon2_volume_cm3 / 1_000_000
echantillon2_densite = echantillon2_masse_en_kg / echantillon2_volume_m3
echantillon3_masse_en_kg = echantillon3_masse_en_g / 1000
echantillon3_volume_m3 = echantillon3_volume_cm3 / 1_000_000
echantillon3_densite = echantillon3_masse_en_kg / echantillon3_volume_m3
#Affichage des résultats
print("Densité 1 :", round(echantillon1_densite, 2), "kg/m3")
print("Densité 2 :", round(echantillon2_densite, 2), "kg/m3")
print("Densité 3 :", round(echantillon3_densite, 2), "kg/m3")
Lorsqu'on exécute la version originale du code, ou votre version améliorée, on devrait observer le même résultat dans la console.
Dans la documentation du module time (doc), on trouve la fonction time.monotonic_ns().
Cette fonction permet d'obtenir le temps en nanosecondes depuis le lancement de l'application. À chaque appel de la fonction, le temps retourné est toujours de plus en plus grand. Testez le code ci-dessous :
import time
print(f"Temps moment A: {time.monotonic_ns()}")
print(f"Temps moment B: {time.monotonic_ns()}")
print(f"Temps moment C: {time.monotonic_ns()}")
Maintenant que vous comprennez ce que retourne cette fonction, observez son utilisation ci-dessous :
import time
def calcul_intensif():
'''
N'essayez VRAIMENT pas de comprendre le code de cette fonction!
Vous allez être en mesure de le comprendre à partir du cours sur les boucles.
La seule chose qui est importante de savoir, c'est que cette fonction prend un
certain temps pour s'exécuter (1 à 2 secondes en moyenne).
'''
total = 0
for i in range(1, 20000000): # 20 millions d'itérations
total += i ** 0.5
return total
tempA = time.monotonic_ns()
calcul_intensif()
tempB = time.monotonic_ns()
mystere = tempB - tempA # Expression intéressante
print(mystere)
Question
✏️ Selon vous, en observant les instructions 15 à 19, que représente le nombre contenu dans la variable mystere?
Instructions pour vous aider dans votre réflexion
- Exécutez le programme tel quel et notez la valeur affichée.
- À la ligne 11, modifiez le nombre 20 000 000 pour 40 000 000.
- Réexécutez le programme et notez le nouveau résultat.
- Expliquez la différence entre les 2 résultats obtenus.
🎯 Solutions des exercices
Un solutionnaire possible pour chaque exercice est disponible en format vidéo avec des explications. Vous pouvez vous en servir pour comparer votre solution avec une solution possible jugée optimale et vous débloquer après un long moment bloqué sur un exercice (ex. 20 minutes) et après avoir utilisé le dégogueur pour essayer par vous-même de trouver le problème.
Il est tout à fait normal que certains problèmes demandent du temps, de la réflexion, et parfois même un peu de frustration. C’est précisément dans ces moments d’effort que l’apprentissage s’ancre réellement.
Consulter un solutionnaire avant d’avoir tenté l’exercice par soi-même, ou le parcourir trop rapidement, revient à court-circuiter le processus d’apprentissage. Ce n’est pas simplement contre-productif, c’est pédagogiquement désastreux.
En sautant l’étape de la réflexion personnelle, on prive son cerveau de l’occasion de construire des connexions durables. Et à force de répéter ce réflexe, on risque de passer à côté des compétences essentielles, ce qui peut mener à des échecs plus tard, même si tout semble facile sur le moment. Alors oui, prenez le temps. L’erreur fait partie du jeu. C’est en cherchant, en tâtonnant, en doutant, qu’on devient réellement compétent. Le solutionnaire doit être un outil de validation, pas un raccourci.
🔨 Solution des exercices de création :
La récursivité est une notion plus avancée qui dépasse le cadre de ce cours.
Elle n'est pas obligatoire pour réussir le cours, mais il s'agit d'un concept intéressant à explorer si vous êtes curieu.x.se.
Vous pouvez choisir de ne pas lire cette section si vous n'êtes pas assez à l'aise ou si vous êtes déjà assez mêlé.e comme ça!
La récursivité est une technique de programmation où une fonction s'appelle elle-même pour résoudre un problème.
Cela peut être utile pour résoudre des problèmes qui peuvent être décomposés en sous-problèmes similaires.
Voici un exemple simple de fonction récursive qui calcule la factorielle d'un nombre :
(note : le code contient un if que l'on n'a pas encore vu, mais c'est pour illustrer la récursivité)
def factorielle(n):
if n == 0 or n == 1: # Cas de base
return 1
else:
return n * factorielle(n - 1) # Appel récursif
print(factorielle(5)) # Affiche 120
Dans cet exemple, la fonction factorielle s'appelle elle-même avec un paramètre réduit jusqu'à atteindre le cas de base (0 ou 1), où elle retourne 1.
La pile d'appels se remplit à chaque appel récursif, puis se vide lorsque les appels sont résolus.
Si vous êtes curieu.x.se vous pouvez exécuter ce code en mode débogage et observer la pile d'appels pour voir comment elle évolue avec chaque appel récursif.