🔍 Expressions booléennes

Qu'est-ce qu'une expression booléenne?

Une expression booléenne est une expression qui évalue à une valeur de vérité (bool), c'est-à-dire soit True (vrai) soit False (faux).
Elles sont utilisées pour prendre des décisions dans le code, comme dans les instructions conditionnelles (if, elif, else) et les boucles (while, for).

Opérateurs de comparaison

Les opérateurs de comparaison sont utilisés pour comparer deux valeurs.
Voici les principaux opérateurs de comparaison en Python :

Opérateur	Description	Exemple	Résultat
`==`	Égal à	`a == b`	`True` si `a` est égal à `b`, sinon `False`
`!=`	Différent de	`a != b`	`True` si `a` est différent de `b`, sinon `False`
`<`	Inférieur à	`a < b`	`True` si `a` est inférieur à `b`, sinon `False`
`<=`	Inférieur ou égal à	`a <= b`	`True` si `a` est inférieur ou égal à `b`, sinon `False`
`>`	Supérieur à	`a > b`	`True` si `a` est supérieur à `b`, sinon `False`
`>=`	Supérieur ou égal à	`a >= b`	`True` si `a` est supérieur ou égal à `b`, sinon `False`

Exemples d'utilisation

a = 5
b = 10
print(a < b)   # Affiche True
print(a == b)  # Affiche False
print(a + 5 >= b - max(1, min(4, a, 6), 5))   # Affiche False, explications ci-dessous!

Les 2 opérandes d’un opérateur de comparaison peuvent être le résultat de l'évaluation d’expressions.
Python évalue l’expression selon la priorité des opérateurs, en remplaçant chaque sous-expression par sa valeur résultante.

Voici comment Python évalue l’instruction #5, étape par étape :

print(a + 5 >= b - max(1, min(4, a, 6), 5))  # Instruction originale
print(5 + 5 >= b - max(1, min(4, 5, 6), 5))  # Remplace 'a' par sa valeur
print(10 >= b - max(1, min(4, 5, 6), 5))     # Calcule la somme de '5 + 5'
print(10 >= 10 - max(1, min(4, 5, 6), 5))    # Remplace 'b' par sa valeur
print(10 >= 10 - max(1, 4, 5))               # La fonction min(...) doit être résolue avant la fonction max(...)
print(10 >= 10 - 5)                          # La fonction max(...) est résolue
print(10 >= 5)                               # L'opération >=
print(True)                                  # Affiche "True" dans la console

Opérateurs logiques

Les opérateurs logiques sont utilisés pour combiner plusieurs expressions booléennes.
Voici les principaux opérateurs logiques en Python :

Opérateur	Description	Exemple	Résultat
`and`	ET logique	`a and b`	`True` si `a` et `b` sont tous deux `True`, sinon `False`
`or`	OU logique	`a or b`	`True` si au moins un de `a` ou `b` est `True`, sinon `False`
`not`	NON logique	`not a`	`True` si `a` est `False`, sinon `False`

Priorité des opérateurs

La priorité des opérateurs détermine l'ordre dans lequel les opérations sont effectuées dans une expression.
En Python, la priorité des opérateurs est la suivante (de la plus haute à la plus basse) :

Parenthèses ()
Opérateurs de comparaison (==, !=, <, <=, >, >=)
Opérateur not
Opérateur and
Opérateur or

Un ordre plus exhaustif des priorités des opérateurs est disponible ici dans l'aide-mémoire.

Exemple de priorité

a = 5
b = 10
c = 15
print(a < b and b < c)  # Évalué comme (a < b) and (b < c), affiche True
print(a < b or b > c)   # Évalué comme (a < b) or (b > c), affiche True
print(not a < b)        # Évalué comme not (a < b), affiche False

# On peut utiliser des parenthèses pour modifier l'ordre d'évaluation :
print(a < b or b > c and a == 5)  # Évalué comme a < b or (b > c and a == 5), affiche True
print((a < b or b > c) and a == 5) # Évalué comme (a < b or b > c) and a == 5, affiche True

Stockage dans des variables

On peut stocker le résultat d'une expression booléenne dans une variable pour une utilisation ultérieure.

a = 5
b = 10
est_plus_petit = a < b  # est_plus_petit sera True
est_egal = a == b       # est_egal sera False
print(est_plus_petit)    # Affiche True
print(est_egal)          # Affiche False

Autres opérateurs d'expression booléenne

Voici quelques autres opérateurs d'expression booléenne utiles en Python :

Opérateur	Description	Exemple	Résultat
`in`	Appartenance (contenu dans)	`"a" in "chat"`	`True`
`not in`	Non-appartenance (pas dans)	`"b" not in "chat"`	`True`

Exemple d'utilisation

mot = "chat"
print("a" in mot)      # Affiche True
print("b" not in mot)  # Affiche True

On veut pas le sawouère, on veut le wouère

C'est bien beau, ça, les expressions booléennes, mais à quoi ça sert?
👉 Elles servent principalement à contrôler le flux d'exécution du programme,
c'est-à-dire à décider quelles parties du code doivent être exécutées en fonction de certaines conditions.

Structure de base d'une instruction conditionnelle

Voici un exemple simple d'instruction conditionnelle en Python :

age = 18
if age >= 18 :
    print("Vous êtes majeur.")

Dans cet exemple, l'instruction if vérifie si la variable age est supérieure ou égale à 18.
Si c'est le cas (si la condition est True), le code indenté sous l'instruction if est exécuté, affichant "Vous êtes majeur.".
Si la condition est False, le code indenté n'est pas exécuté.

Indentation

En Python, l'indentation (les espaces ou tabulations avant une ligne de code) est cruciale pour définir les blocs de code.
Le code qui doit être exécuté conditionnellement doit être indenté sous l'instruction if.
Par exemple :

if condition :
    # Code indenté, exécuté si la condition est True
    faire_quelque_chose_conditionnel()
    faire_autre_chose_conditionnel()
# Code non indenté, exécuté indépendamment de la condition
faire_autre_chose_en_tout_temps()

Exemple d'erreur courante due à une mauvaise indentation :

if condition :
faire_quelque_chose()  # Erreur : cette ligne doit être indentée

Exemple concret :

age = 20
if age >= 18 :
    print("Vous êtes majeur.")
    print("Vous avez le droit de vote!")
    print("Un grand pouvoir implique de grandes responsabilités.")
print("Bienvenue!")  # Toujours exécuté, indépendamment de l'âge

Un elfe?

Non!
elif est la contraction de "else if", qui signifie "sinon si".
Elle permet de vérifier une autre condition si la première condition dans l'instruction if est False.

Par exemple :

age = 16
if age >= 18 :
    print("Vous êtes majeur.")
elif age >= 13 :
    print("Vous êtes adolescent.")

Multiple elif

On peut avoir plusieurs clauses elif pour vérifier plusieurs conditions différentes.
Par exemple :

age = 10
if age >= 18 :
    print("Vous êtes majeur.")
elif age >= 13 :
    print("Vous êtes adolescent.")
elif age >= 3 :
    print("Vous êtes un enfant.")

Ordre des conditions

L'ordre des conditions est important.
Les conditions sont évaluées de haut en bas, et la première condition qui est True déclenche l'exécution du bloc de code correspondant.
Par exemple, dans le code suivant, la condition age >= 13 sera toujours True pour tous les adultes, et la condition age >= 18 ne sera jamais atteinte :

age = 21
if age >= 13 :
    print("Vous êtes adolescent.")
elif age >= 18 :
    print("Vous êtes majeur.")

Pour éviter cela, il faut toujours commencer par la condition la plus restrictive (la plus élevée) et descendre vers les conditions moins restrictives :

age = 21
if age >= 18 :
    print("Vous êtes majeur.")
elif age >= 13 :
    print("Vous êtes adolescent.")

Pas de elif sans if

Une clause elif doit toujours être précédée d'une instruction if.
Par exemple, le code suivant est incorrect et provoquera une erreur de syntaxe :

age = 16
elif age >= 13 :  # Erreur : 'elif' sans 'if'
    print("Vous êtes adolescent.")

Le sinon

else signifie "sinon".
Elle permet de définir un bloc de code qui sera exécuté si toutes les conditions précédentes (if et elif) sont False.

Par exemple :

age = 10
if age >= 18 :
    print("Vous êtes majeur.")
elif age >= 13 :
    print("Vous êtes adolescent.")
else :
    print("Vous êtes un enfant.")

Dans cet exemple, si age est inférieur à 13, le message "Vous êtes un enfant." sera affiché.

Utilisation avec if et elif

La clause else est souvent utilisée à la fin d'une série d'instructions if et elif pour capturer tous les cas non couverts par les conditions précédentes.
Par exemple :

score = 85
if score >= 90 :
    print("Excellent")
elif score >= 75 :
    print("Bien")
elif score >= 50 :
    print("Passable")
else :
    print("Échec")

Pas de condition avec else

Contrairement à if et elif, la clause else ne prend pas de condition.
Elle est simplement exécutée si toutes les conditions précédentes sont False. Par exemple, le code suivant est incorrect et provoquera une erreur de syntaxe :

score = 85
if score >= 90 :
    print("Excellent")
elif score >= 75 :
    print("Bien")
elif score >= 50 :
    print("Passable")
else score < 50 :  # Erreur : 'else' ne doit pas avoir de condition
    print("Échec")

else sans elif

Il est possible d'utiliser else directement après un if, sans avoir besoin de elif.
Par exemple :

age = 20
if age >= 18 :
    print("Vous êtes majeur.")
else :
    print("Vous êtes mineur.")

Intégration avec des fonctions

Les structures conditionnelles (if/elif/else, match/case) peuvent être utilisées à l'intérieur de fonctions.
Par exemple :

def est_pair(n):
    if n % 2 == 0:
        return True  # Faire modulo 2 sur un nombre pair donne toujours 0!
    else:
        return False

a = 33
b = 52
print(f"{a} est un nombre pair : {est_pair(a)}")
print(f"{b} est un nombre pair : {est_pair(b)}")

Cet exemple permet de calculer la paie brute d'un employé :

def calculer_paie_brute(nb_heures, taux_horaire, temps_double_apres_40_heures=False):
    salaire = nb_heures * taux_horaire
    if temps_double_apres_40_heures and nb_heures >= 40:
        nb_heures_temps_supp = nb_heures - 40
        salaire = salaire + nb_heures_temps_supp * taux_horaire * 2
    return salaire

nb_heures = 45
taux_horaire = 20
print(f"Calcul de la paie brute pour {nb_heures} heures à un taux horaire de {taux_horaire}$/h.")
print(f"  Avec le temps > 40 payé au taux doublé : {calculer_paie_brute(nb_heures, taux_horaire, True)}$")
print(f"  Avec le temps > 40 payé au taux régulier : {calculer_paie_brute(nb_heures, taux_horaire)}$")

Récapitulatif if, elif, else

Pour récapituler, la structure d'une instruction conditionnelle en Python est la suivante :

if : Obligatoire pour commencer une instruction conditionnelle.
elif : Optionnels, il peut y en avoir 0, 1, 2, ou plus.
Chaque elif vérifie une condition, seulement si toutes les conditions précédentes sont False.
else : Optionnel, il n'y a qu'un seul else possible.
Il est exécuté si toutes les conditions précédentes sont False.
Ne prend pas de condition.

Autres points importants à retenir

Indentation : le code à exécuter conditionnellement doit être indenté sous l'instruction correspondante.
Ordre des conditions : les conditions sont évaluées de haut en bas, la première condition True déclenche l'exécution du bloc de code correspondant, et les autres sont ignorées.

Forme compacte

Pour les instructions conditionnelles simples, on peut utiliser une forme compacte en une seule ligne.
Par exemple :

age = 20
print("Vous êtes majeur.") if age >= 18 else print("Vous êtes mineur.")

On peut aussi utiliser cette forme compacte pour stocker le résultat dans une variable :

age = 20
statut = "majeur" if age >= 18 else "mineur"
print(statut)  # Affiche "majeur"

Limites de la forme compacte

La forme compacte est utile pour des conditions simples et des actions courtes.
Cependant, pour des conditions plus complexes ou des blocs de code plus longs,
il est préférable d'utiliser la forme standard avec indentation pour une meilleure lisibilité.

Avec des elif

On peut aussi utiliser des elif dans une forme compacte, mais cela peut rapidement devenir difficile à lire.
Par exemple :

score = 85
resultat = "Excellent" if score >= 90 else "Bien" if score >= 75 else "Passable" if score >= 50 else "Échec"
print(resultat)  # Affiche "Bien"

Si on a besoin de elif, il est préférable d'utiliser la forme standard pour une meilleure lisibilité.

match/case

Le match/case est une structure de contrôle qui permet de faire des correspondances de motifs (pattern matching).

Il permet de comparer une variable à plusieurs valeurs possibles.
Il offre ainsi une alternative aux longues chaînes d'instructions if/elif/else pour des cas spécifiques.

Sa syntaxe est la suivante :

match variable:
    case valeur1:
        # code à exécuter si variable == valeur1
    case valeur2:
        # code à exécuter si variable == valeur2
    case _:
        # code à exécuter si aucune des valeurs précédentes ne correspond

Le _ dans le dernier case agit comme un else, capturant tous les autres cas non spécifiés.
Utile pour des comparaisons simples, mais peut être moins flexible que if/elif/else pour des conditions complexes.
Exemple :

jour = "lundi"
match jour:
    case "lundi":
        print("Début de la semaine")
    case "mercredi":
        print("Milieu de la semaine")
    case "vendredi":
        print("Fin de la semaine")
    case _:
        print("Jour ordinaire")

Avantages du match/case

Plus lisible pour des comparaisons multiples sur une même variable.
Permet de gérer facilement des cas spécifiques.
Peut être plus performant que de nombreuses instructions if/elif dans certains cas.

👉 Il est important de noter que tout match/case peut être réécrit avec des if/elif/else, mais l'inverse n'est pas toujours vrai.

Pourquoi des exceptions?

Quand un programme rencontre une erreur (division par zéro, fichier manquant, format invalide),
Python interrompt son exécution avec un message d’erreur. Ces erreurs sont appelées exceptions.

Avec try et except, on peut contrôler ce qui se passe en cas d’erreur, au lieu de laisser le programme planter.

Exemple de base : division par zéro

Copiez et exécutez ce code :

numerateur = 10
denominateur = 0
resultat = numerateur / denominateur

Notez l’erreur affichée par Python.

Maintenant, modifiez le code pour gérer l’erreur, et exécutez-le en mode débogage, ligne par ligne, afin de bien comprendre le flux d’exécution :

numerateur = 10
denominateur = 0

try :
    resultat = numerateur / denominateur
    print("Résultat:", resultat)
except ZeroDivisionError :
    print("Erreur : division par zéro interdite.")

Grâce au try/except, on affiche plutôt un message clair à l’utilisateur et le programme continue.

Différence entre try/except et raise

try/except = rattraper une erreur qui se produit (mettre un filet de sécurité).
raise = provoquer volontairement une erreur si une condition n’est pas respectée (mettre une barrière).

Lever une erreur soi-même (raise)

On peut aussi créer nos propres erreurs quand les conditions ne sont pas respectées.

def concentration(masse_g, volume_L):
    if volume_L == 0 :
        raise ZeroDivisionError("Le volume ne peut pas être 0.")
    if masse_g < 0 :
        raise ValueError("La masse doit être positive.")
    return masse_g / volume_L

Dans ce cas, l’erreur est volontaire : on empêche l’utilisation de valeurs impossibles en science.

Intercepter une erreur personnalisée (try/except)

Si on souhaite intercepter l'erreur avec le message d'erreur personnalisé, on doit utiliser un bloc try/except comme ceci :

try:
    # Début du code à risque
    concentration(4,20)         # OKI, éxécuté  sans problème
    concentration(-10,20)       # PAS OKI, masse négative!
    concentration(4,20)         # JAMAIS éxécuté à cause de l'exception
    # Fin du code à risque
except (ZeroDivisionError, ValueError) as e:
    # Interception de l'erreur
    print(f"Une erreur est subvenue : {e}")

La variable e contient ici l'exception interceptée, l'afficher à la console va afficher le message d'erreur personnalisé.

Bonnes pratiques

N’attrapez que les erreurs prévues (sinon on cache de vrais bogues).
Donnez toujours un message utile qui aide à corriger.
Utilisez raise pour signaler un problème clair à l’utilisateur qui utilise votre fonction.

Catégories d'exception utilisées pour ce cours

Dans ce cours, nous allons nous limiter à utiliser les exceptions déjà existantes les plus communes :

ZeroDivisionError : une division par zéro.
TypeError : le type de la donnée transmise à la fonction n'est pas du type attendu.
ValueError : la valeur transmise à la fonction n'est pas cohérente avec ce qui est attendu.

Pour aller plus loin

Il est aussi possible de créer ses propres types d’erreurs en définissant une classe qui hérite de Exception.
Comme mentionné précédemment, nous allons nous limiter aux exceptions déjà existantes, mais sachez que cette possibilité existe.
C’est utile dans de grands projets pour distinguer vos erreurs spécifiques de celles de Python.

Exemple minimal :

class DonneesInvalidesError(Exception): pass # Définir un nouveau type d'erreur

raise DonneesInvalidesError("Les données fournies ne sont pas valides.")

Valider les paramètres

Quand on écrit une fonction, il faut s’assurer que les entrées (paramètres) ont du sens.
Sinon, on risque d’obtenir des résultats absurdes ou des erreurs difficiles à comprendre.

En science, valider les paramètres est essentiel pour pouvoir faire confiance aux calculs.
Exemple : vérifier qu’une masse est positive, qu’un volume n’est pas nul, etc.

Validation et exceptions

Validation = vérifier les entrées avant de calculer.
Exceptions = signaler clairement un problème si les conditions ne sont pas respectées.

👉 La validation utilise souvent raise pour bloquer une fonction quand un paramètre est invalide.

Exemple : calcul de densité

Version 1 – sans validation

def densite(masse, volume):
    return masse / volume

print(densite(10, 2))   # 5.0
print(densite(8, 0))    # Erreur Python (division par zéro)

Ici, la fonction ne réalise pas de validation, alors le programme plante si on entre un volume nul ou une masse invalide, avec des messages d'erreur génériques.

Version 2 – avec validation

def densite(masse, volume):
    if masse < 0:
        raise ValueError("La masse doit être positive.")
    if volume <= 0:
        raise ZeroDivisionError("Le volume doit être supérieur à 0.")
    return masse / volume

print(densite(10, 2))   # 5.0
print(densite(-3, 5))   # ValueError
print(densite(8, 0))    # ZeroDivisionError

Ici, la fonction effectue des validations et lève des exceptions accompagnées de messages d'erreur clair et précis, selon la situation problématique détectée.

Pourquoi valider?

Les erreurs deviennent explicites (ex.: “volume doit être > 0”).
On évite les résultats absurdes.
Le code est plus robuste et réutilisable.

Mini checklist de validation

✅ Types corrects (int, float)
✅ Domaines respectés (positif, non nul)
✅ Cas limites couverts (valeur négative, zéro, etc.)

Exemple complet avec validation et exceptions

Voici un exemple complet d'une fonction qui calcule la concentration d'une solution, avec validation des paramètres et gestion des exceptions :

def calculer_concentration(masse_g, volume_L):
    if not isinstance(masse_g, (int, float)):
        raise TypeError("La masse doit être un nombre (int ou float).")
    if not isinstance(volume_L, (int, float)):
        raise TypeError("Le volume doit être un nombre (int ou float).")
    if masse_g < 0:
        raise ValueError("La masse doit être positive.")
    if volume_L <= 0:
        raise ValueError("Le volume doit être supérieur à 0.")
    return masse_g / volume_L

# Exemples d'utilisation
try:
    print(calculer_concentration(10, 2))    # 5.0
    print(calculer_concentration(-5, 2))    # ValueError
    print(calculer_concentration(10, 0))    # ValueError
    print(calculer_concentration(10, "a"))  # TypeError
except (TypeError, ValueError) as e:
    print(f"Erreur : {e}")

La fonction isinstance(valeur, type) permet de vérifier si une certaine valeur est bien d'un certain type.
Par exemple isinstance(5, int) retourne True alors que isinstance("5", int) retourne False.
Dans l'exemple, il est vérifié si les paramètres sont de type int ou float.

✏️ Exercices de compréhension

Pour faire les traces des exercices suivants, regardez d'abord ces recettes de traces :

Exercice - Trace if/else + forme compacte

Sans exécuter le code, qu'affichera le programme ci-dessous?
En suivant cette recette de trace, faites la trace de l'exécution.
En situation d'examen, ce type de question serait à faire sans l'ordinateur.

def carre(x):
    return x * x

def calcul(n):
    if n % 2 == 0:
        return n + 5
    else:
        return carre(x) - 1

x = 3
x = calcul(x)
if x >= 5:
    calcul(x)
print("Hello World") if x == 13 else print("Fin")

Validez votre trace en exécutant le code dans un script en mode débogage.

Exercice - Trace if/elif/else + forme compacte

def mystere(n):
    print("---")
    if n % 2 == 0:
        print("!")
    elif n >= 10:
        print("E")
        if n // 10 == 5:
            print("X")
        else:
            print("D")
        print("P.")
    elif n >= 20:
        print("F")
    else:
        print("3") if n < 5 else print("33")

mystere(55)
mystere(5)
mystere(12)

Validez votre trace en exécutant le code dans un script en mode débogage.

Exercice - Trace avec opérateurs and et or

def mystere(x, y, z):
    print(f"--- x:{x}, y:{y}, z:{z}")
    if (x >= 5 or y < 15) or z >= 10 :
        print("Condition 1")
    if (x >= 5 and y < 15) or z >= 10 :
        print("Condition 2")
    if (x >= 5 and y < 15) and z >= 10 :
        print("Condition 3")

mystere(0, 5, 5)
mystere(5, 5, 5)
mystere(5, 10, 10)

Validez votre trace en exécutant le code dans un script en mode débogage.

Exercice - Trace avec exception

def calcul(a, b):
    print(f"a : {a} b : {b}")
    if a ** 2 > 20:
        raise ValueError("Valeur interdite")
    return a * b

print("World")
try:
    calcul(2, 3)
    calcul(5, 3)
    calcul(8, 3)
except ValueError as e:
    print(f"Erreur : {e}")
print("Hello")

Validez votre trace en exécutant le code dans un script en mode débogage.

🔨 Exercices de création

Exercice - Le niveau de pH

Définissez une fonction décrivant le niveau d'acidité d'une solution à partir de son pH.
La fonction doit recevoir en entrée le pH et renvoyer en sortie soit : "acide", "neutre" ou "basique".
Validez le bon fonctionnement en testant les différents cas possibles à l'aide d'appels :

print(f"Une solution avec un Ph de 5 est : {nom_de_votre_fonction(5)}") 
print(f"Une solution avec un Ph de 7 est : {nom_de_votre_fonction(7)}")
print(f"Une solution avec un Ph de 10 est : {nom_de_votre_fonction(10)}")

Remarque : si vous obtenez comme résultat "Une solution avec un Ph de 5 est : None" c'est que votre fonction ne retourne pas une valeur!

Exercice - Validation de paramètres

Écrivez une fonction densite(masse, volume) qui retourne la densité en g/mL.

Validez que la masse est positive.
Validez que le volume est strictement positif (non nul).
Levez une exception claire (ValueError ou ZeroDivisionError) si les conditions ne sont pas respectées.

Testez votre fonction en l'appelant avec des valeurs valides et invalides pour vérifier que la validation fonctionne correctement.

Pourquoi est-il préférable d’arrêter l’exécution avec un message clair plutôt que de laisser Python planter avec une erreur brute?

Exercice - SOLUTIONS D'UNE EQUATION QUADRATIQUE

Une équation quadratique, aussi appelée équation du second degré, est une équation polynomiale de la forme $ax² + bx + c = 0$ , où $a$ , $b$ , et $c$ sont des constantes et $a$ est différente de zéro.

Le discriminant $\Delta = b^2 - 4ac$ est crucial pour déterminer le nombre de solutions d'une équation quadratique :

\text{Si} \begin{cases} \Delta > 0, & \text{il y a deux solutions réelles distinctes,} \\ \Delta = 0, & \text{il y a une seule solution réelle,} \\ \Delta < 0, & \text{il n'y a pas de solution réelle, mais il y a deux solutions complexes conjuguées.} \end{cases}

👉 Nous allons nous concentrer uniquement sur les solutions réelles dans cet exercice.

La formule pour trouver les zéros est :

x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

Écrivez un programme permettant d'afficher les solutions d'une équation quadratique.
Votre programme doit demander à l'utilisateur une valeur pour a, b et c et ensuite il doit afficher les solutions.
Faite des variables globales pour stocker les valeurs de a, b et c. Ne créez pas de fonction pour ce numéro.

✅ EXEMPLE DE SORTIE ATTENDUE POUR LES 3 CAS POSSIBLES

Si aucune solution (ex : a = 1, b = 2, c = 5)

Il n'y a pas de solution réelle pour ces valeurs de a, b et c.

Si une seule solution (ex. a = 1, b = 6, c = 9)

Il y a une seule solution (racine double) : -3

Si 2 solutions possibles pour ce problème (ex. a = 1, b = 5, c = 6)

Il y a 2 solutions possibles : -2 et -3

Exercice - Remplacer des instructions

Pour cet exercice, vous devez remplacer les if/elif/else du code ci-dessous par un match/case.

def type_animal(deplacement):
    if deplacement == "vole":
        return "oiseau"
    elif deplacement == "nage":
        return "poisson"
    elif deplacement == "marche":
        return "mammifère"
    elif deplacement == "rampe":
        return "reptile"
    else:
        return "inconnu"

deplacement = "vole"
print(f"Si je {deplacement}, je suis un {type_animal(deplacement)}.")

Exercice - Calcul de la note finale du cours, avec la double sanction!

Améliorez le code réalisé lors de la rencontre 2 servant à calculer la note finale du cours.

Créez une fonction :
- qui prend en paramètres les 4 nombres représentant les notes,
- et qui retourne la note finale calculée.
Appelez cette fonction pour réaliser le calcul avec les notes saisies.
Modifiez le calcul de la note finale afin de prendre en compte la double sanction.

Double sanction : Pour réussir le cours, la personne étudiante doit conserver un minimum de 60% aux évaluations supervisées (examens, contrôles) ainsi qu’un minimum de 60% aux évaluations non supervisées (travaux pratiques, devoirs). À défaut de répondre à ces exigences, la personne étudiante obtient, à son bulletin, la note la plus basse enregistrée : celle des évaluations supervisées ou celle des évaluations non supervisées.

Exercice - Gènes Myc et P21 🧬

Les gènes Myc et p21 régulent le cycle cellulaire de manière opposée : Myc stimule la prolifération cellulaire en activant des gènes liés à la croissance, tandis que p21 freine cette progression en bloquant les enzymes responsables de la division. On les étudie en science parce qu’ils jouent un rôle clé dans le développement du cancer, Myc par sa capacité à favoriser les tumeurs, et p21 par son potentiel à les empêcher. Ces 2 gènes exercent souvent des effets opposés dans les cellules souches.

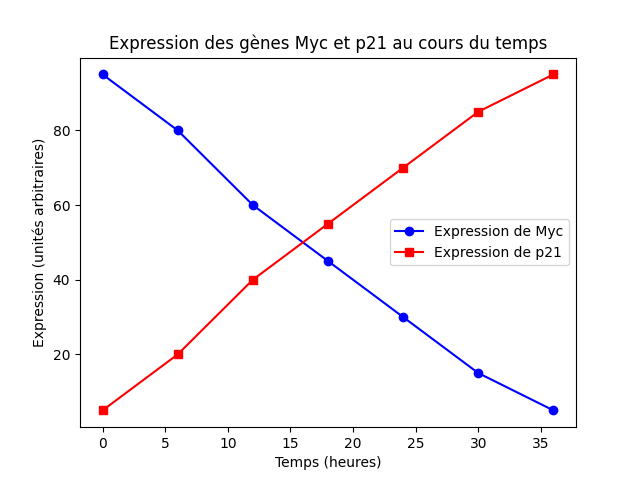
Les deux courbes se croisent entre 12h et 24h, c’est le point d’équilibre!
Ce moment marque une transition biologique importante : la cellule quitte son état prolifératif pour entrer en phase de différenciation.

📊 Étape A - Recréez le graphique, à vous de jouer!

Utilisez Python pour générer le graphique, et rien d’autre! Même si la bibliothèque Matplotlib n’a pas encore été abordée, vous disposez d’un exemple suffisamment clair pour vous guider. Il ne vous reste qu’à l’adapter à notre contexte. Pour le moment pas besoin de ChatGPT 🤖, vous avez déjà tout ce qu’il faut pour réussir cette étape!

Voici les données nécessaires pour réaliser cette tâche :

'''
Les valeurs stockées dans ces variables sont des listes,
structure de donnéees que nous verrons plus tard dans le cours.
Pour l'instant, contentez-vous de copier-coller ces lignes dans votre script.
 '''
temps = [0, 6, 12, 18, 24, 30, 36]          # Valeurs en X pour les 2 gènes
exp_gene_myc = [95, 80, 60, 45, 30, 15, 5]  # Valeurs en Y pour le gène Myc
exp_gene_p21 = [5, 20, 40, 55, 70, 85, 95]  # Valeurs en Y pour le gène p21

🤖 Étape B - Expérimentez avec l'aide de ChatGPT!

💡 Instructions pour cette section

Commencez par interroger ChatGPT afin de bien comprendre le rôle de chaque ligne de code présentée.
Une fois que vous êtes certain de leur fonctionnement, intégrez-les progressivement dans votre propre script.
Voici le résultat souhaité :

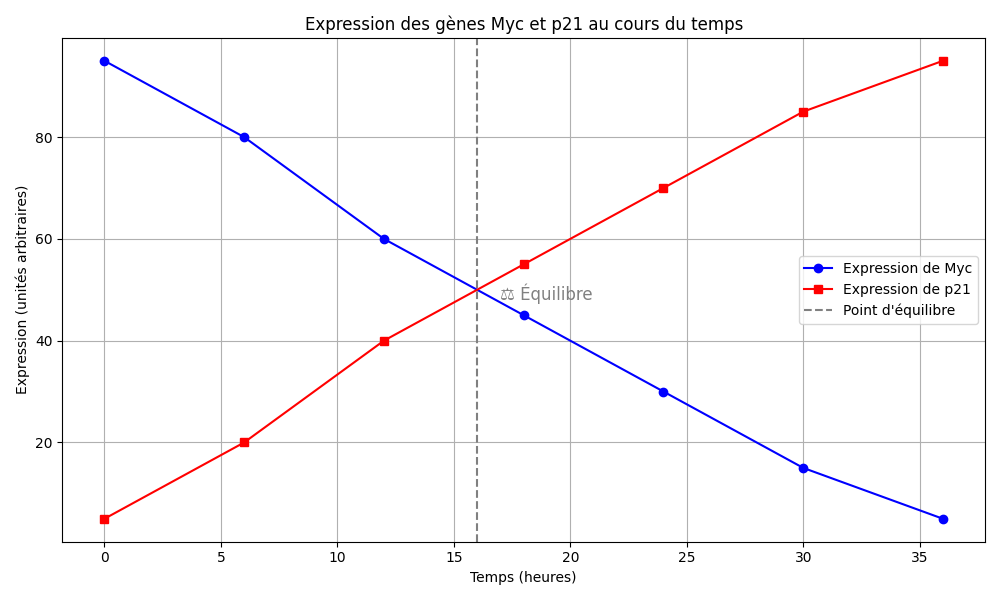
⚙️ Procédez étape par étape

Ajoutez et relancez le programme à chaque changement afin de bien voir les changements.

# Mettre immédiatement après la création des tableaux de données
plt.figure(figsize=(10, 6))

# Mettre n'importe où avant l'instruction plt.show()
plt.tight_layout()

# Mettre n'importe où avant l'instruction plt.show()
plt.grid(True)

# Mettre n'importe où avant l'instruction plt.show()
plt.axvline(x=16, color='gray', linestyle='--', label='Point d\'équilibre')

# Mettre n'importe où avant l'instruction plt.show()
plt.text(17, 48, '⚖️ Équilibre', fontsize=12, color='gray')

# Remplacer plt.show() par cette instruction, lancer le programme, puis ouvrir le fichier ".png" généré
plt.savefig('image_du_graphique.png')

🎯 Solutions des exercices

Un solutionnaire possible pour chaque exercice est disponible en format vidéo avec des explications. Vous pouvez vous en servir pour comparer votre solution avec une solution possible jugée optimale et vous débloquer après un long moment bloqué sur un exercice (ex. 20 minutes) et après avoir utilisé le dégogueur pour essayer par vous-même de trouver le problème.

attention

Il est tout à fait normal que certains problèmes demandent du temps, de la réflexion, et parfois même un peu de frustration. C’est précisément dans ces moments d’effort que l’apprentissage s’ancre réellement.

Consulter un solutionnaire avant d’avoir tenté l’exercice par soi-même, ou le parcourir trop rapidement, revient à court-circuiter le processus d’apprentissage. Ce n’est pas simplement contre-productif, c’est pédagogiquement désastreux.

En sautant l’étape de la réflexion personnelle, on prive son cerveau de l’occasion de construire des connexions durables. Et à force de répéter ce réflexe, on risque de passer à côté des compétences essentielles, ce qui peut mener à des échecs plus tard, même si tout semble facile sur le moment. Alors oui, prenez le temps. L’erreur fait partie du jeu. C’est en cherchant, en tâtonnant, en doutant, qu’on devient réellement compétent. Le solutionnaire doit être un outil de validation, pas un raccourci.

🔨 Solution des exercices de création :
Le niveau de Ph, Validation de paramètres, Solutions d'une équation quadratique,
Remplacer des instructions, Calcul de la note finale d'un cours, Gènes Myc et P21

✏️ Exercices de compréhension​

🔨 Exercices de création​

📊 Étape A - Recréez le graphique, à vous de jouer!​

🤖 Étape B - Expérimentez avec l'aide de ChatGPT!​

💡 Instructions pour cette section​

⚙️ Procédez étape par étape​

🎯 Solutions des exercices

✏️ Exercices de compréhension

🔨 Exercices de création

📊 Étape A - Recréez le graphique, à vous de jouer!

🤖 Étape B - Expérimentez avec l'aide de ChatGPT!

💡 Instructions pour cette section

⚙️ Procédez étape par étape